|
|
Crossing
Ladders
|
|
|
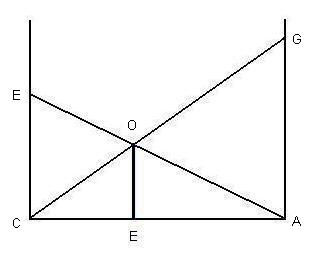
Overview of the SolutionThe classic Crossing Ladders Problem requires a long series of complex formulae and algorithms. We will step through the entire solution in great detail. However, before the details of the solution are described, we will present an overview of the solution, so the you will have some idea of where we are going. Unless you are a mathematician or advanced student, you may want to study this Overview carefully before proceeding to the details of the solution. Visualizing the ProblemAs described in the Introduction, the problem may be visualized like this:
The lines CG, AE and OE are the three given variables, and the object is to find the length AC. Analyzing the TrianglesLook at the diagram above and notice that there are four triangles and that each of the triangle is a right-triangle:
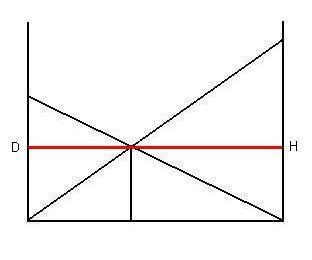
Thus there are four triangles, which can be grouped into two sets of two similar triangles. Each set has a larger triangle and a smaller but similar triangle. Also, we are given only three variables, which make of the legs of the triangles. However, we are given only one side of each of the four triangles. Of course, we need two sides of a triangle to calculate the missing third side using the Pythagorean Theorem. (Note that we are not going to consider angles, except that we know that the four triangles are all right triangles.) Therefore, if we could find a second side of any of these four triangles, then we could solve the problem quickly. If you understand the basics of algebra, geometry and a little trigonometry, then the problem diagrammed above might look reasonably easy to solve, but it is not. As discussed above, the problem starts with two sets of two similar triangles, and we are given only one side of each of these four triangles. We know intuitively that there can be only one solution, because two of the triangles (one from each set of similar triangles) share the same side. That is, AOE and COE share OE as their height. Unfortunately, AOE and COE are not similar triangles. Visualizing the SolutionThe key to the solution of the Classic Ladders Problem (for which Colin Foster deserves full credit) is the realization that the problem cannot be solved in the form diagrammed above. Simply put, there is insufficient information to solve the problem with only the four triangles and three variables. The solution requires the addition of a horizontal line through point O which is parallel to AC, as shown in the following diagram.
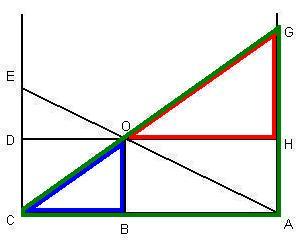
This is the key concept in solving the problem, because the addition of this line creates two additional triangles, OGH and OED. This means that there are now two sets of three triangles which are similar. The following diagram shows that the first set of similar triangles includes CGA, COB and OGH, which are all similar right triangles and whose sides are thus proportional:
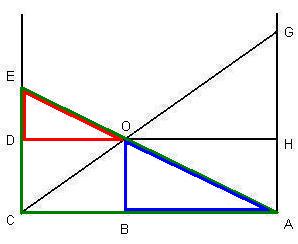
The second set of similar triangles includes AEC, AOB and OED, which again are similar right triangles:
At first, it might appear that the addition of the horizontal line and the two triangles that result from it is not going to be helpful, especially because we do not know any of the sides of these two additional triangles! Yet the analysis of these two additional triangles does provide the key to the solution. We will briefly describe the five steps to the solution. Step 1: Ratio of GH and DEThe first step of the solution is to find the ratio of the heights of the two newly created triangles, OGH and OED. We begin by recognizing the two sets of similar triangles, from which we can determine that the line AB equals the line OD multiplied by the proportional difference in the similar triangles. We determine the ratio of CB to OH and then convert these to determine a second equality for AB. Then we can combine the two equations for AB and simplify them, which produces the ratio of GH and DE. As will be shown below, the key ratio is: Later in the solution, we will have an equation in which we will replace GH with (25 / DE). Step 2: Ratio of AC and DEThe second step of the solution is to find the ratio between AC (the base of both large triangles, which is the object of the problem) and ED (the height of the newly created triangle, OED). The Pythagorean Theorem is applied to the triangle AEC, appropriate substitutions are made, and the ratio between AC and DE is derived. As will be shown in detail below, the key ratio is:
Step 3: Ratio of AC and GHThe third step of the solution is to find the ratio between AC (the base of both large triangles, which is the object of the problem) and GH (the height of the other newly created triangle, OGH). The Pythagorean Theorem is applied to the triangle CGA, appropriate substitutions are made, and the ratio between AC and GH is derived. As will be shown in detail below, the key ratio is:
Step 4: Solve for DEThe fourth step of the solution is to find combine the equations in the second and third step. The right side of the preceding equations are equal, so they are combined and then simplified. Finally, the equation derived in the first step allows us to substitute a term. When these combinations and substitutions are done, the resulting equation contains only a single variable, line DE. Since it contains only a single variable, the equation can be solved. However, because the equation, shown below, is a fourth-order polynomial, the equation requires an algorithmic rather than an analytic solution. 0 = DE4 + 10DE3 - 375DE2 - 250DE - 25 Step 5: Solve for ACThe fifth and final step is the easiest, because we know two of the three sides of the triangle. We now know the lengths of two sides of the right triangle AEC: AE, which is 20; and CE, which is approximately 7. Applying the Pythagorean Theorem, the base AC is shown to be approximately 18.7. The detailed steps are given below, but the solution begins with the key concept of adding a horizontal line through the Point O to create two similar triangles. |
A Note About NotationThe explanation and equations in this solution use Bad Math Notation! Normally, notation such as (AB) refers to a vector rather than magnitude, and notation in the form |AB| denotes magnitude. Here, however, in order to keep the notation as simple as possible, we use the notation (AB), (OD), etc. not as vectors but only as magnitude. For example, CG = 25; AE = 20; and EB = 5.
|