|
|
Crossing
Ladders
|
|
|
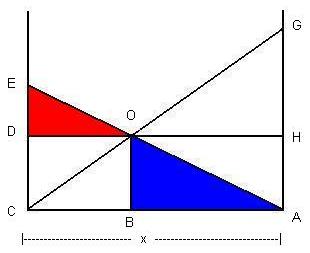
Step 1: Ratio of GH and DESimilar Right-Angle TrianglesThe triangles in the Crossing Ladders Problem are all right triangles. A right triangle means a triangle whose base forms a 90 degree angle from its height. Since the problem assumes that the "walls" and "ruler" are 90 degrees from the "floor", then the triangles which concern us are all right triangles.
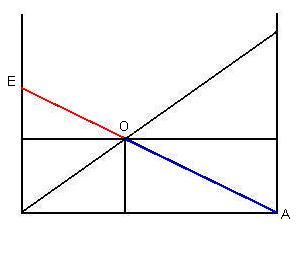
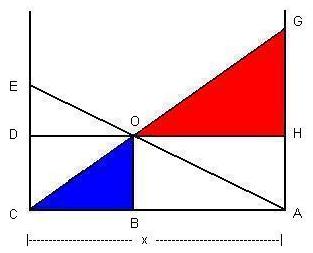
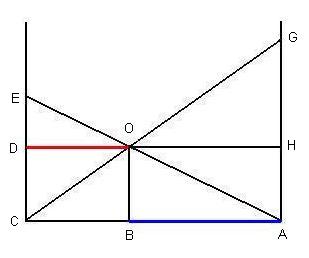
Several of the triangles in the Crossing Ladders Problem are similar. As taught in basic trigonometry, two triangles are similar if they are equally proportional to each other. This means, for example, that a triangle's height is proportional to the height of a similar triangle, as are the triangle's base and hypotenuse. In the Crossing Ladders Problem, we will concentrate on two sets of three similar triangles, which is a total of six different triangles. Note also that each of these four triangles is a right triangle. Triangles AOB and OEDThe first set of similar triangles includes the two triangles shown in the following diagram, in which the blue triangle is similar to the red triangle, which defines the triangles AOB and OED.
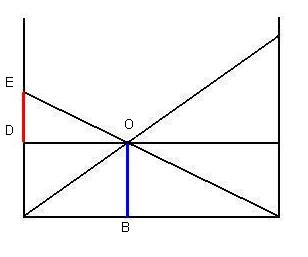
Because the triangles AOB (blue) and OED (red) are similar, we may establish the ratios between the sides of these two triangles. First, we first note the ratio in the following diagram between the blue line (AO) and the red line (EO), which we can express as (AO/EO).
The ratio (AO/EO), as shown in the diagram above, is the same ratio, as shown in the diagram below, between the blue line (OB) and the red line (DE), which we can express as (OB/DE):
The ratios (AO/EO) and (OB/DE), diagrammed above, are the same ratio, as shown in the diagram below, between the blue line (AB) and the red line (DO), which we can express as (AB/DO):
In summary, the triangles AOB (red) and OED (blue) are similar, so the ratios of their sides are equal, as follows:
Triangles COB and OGHThe second set of similar triangles COB (blue) and OGH (red) is shown in the following diagram where, again, the triangles are similar.
Again, remember that similar triangles, as shown in the above diagrams, have proportional bases, heights, and hypotenuses. Therefore, as we did above, we construct the ratios of the sides of the triangles COB and OGH. We find that the triangles COB (blue) and OGH (red) have the following ratios of their sides:
Basic EquationsWe can construct a solution to the Crossing Ladders Problem by solving first either for line (AB) or for line (BC) -- using either line to start the solution will lead to the complete solution. In this case, we elected to begin with line (AB). From the ratios above, we know that line (AB) is similar to line (DO). Thus:
By considering the first set of triangles, AOB and OED, we know that the line AB equals the line DO multiplied by the ratio described above, (OB/DE). Therefore, our first basic equation is:
Now we will make the same calculation with the other set of triangles, COB and OGH. However, we're not looking for the equation for the line CB but for the line AB, so these calculations are more difficult that those above. The analysis is difficult but straightforward. We know that the line CB equals the line OH multiplied by the ratio described above, (OB/GH). Thus:
Now we have a problem: can we find a way to transform the equation above so that is solves for the line AB rather than for the line CB. Look at the diagram above. We start by transposing the equation above by multiplying both sides by (GH):
Now divide both sides by OB:
If we reverse sides and rearrange the terms, we have:
Now we are close to our goal of getting an equation whose terms include only (AB), (CB), (GH) and (OB). First, notice that line (CB) is exactly the same as line (OD). We can thus substitute:
Next, we notice that line (OH) is exactly the same as line (AB). After we make this substitution, we have the second basic equation:
SubstitutionFrom this point onward, only algebra is needed to determine the length of the line AC. Equations (1) and (2) can be rearranged, as follows:
This simplifies, first by dropping OD:
Next, multiply by OB:
and reverse the terms:
We know that the line OB equals 5, so:
This completes Step 1, and we now have the ratio between GH and DE:
|
|